- 最後登錄
- 2025-6-17
- 在線時間
- 2206 小時
- 註冊時間
- 2009-10-20
- 閱讀權限
- 80
- 精華
- 0
- UID
- 7156811
     
- 帖子
- 6642
- 積分
- 33359 點
- 潛水值
- 120493 米
| 本帖最後由 誠惶誠恐 於 2022-6-29 07:18 PM 編輯
The notation used in this article:
B = ♗ Bishop
K = ♔ King
Q = ♕ Queen
R = ♖ Rook
S = ♘ Springer in German = Knight in English
(no character) = ♙ Pawn
What is a Chess Problem?
by Peter Wong
The best games of chess are considered beautiful. They are admired, and replayed around the world by enthusiasts for that reason, apart from the practical use of studying such games. Yet when we play a game, the only real consideration is how to win it, never mind whether the method of winning is attractive or not. But what if we devise a position specifically to demonstrate a beautiful or artistic chess idea? That, in fact, is what occurs in the composition of a chess . When you solve such a problem, its composer’s aesthetic intent is revealed in the play of the solution.
So chess problems – also known as chess – are enjoyed on two levels. On a basic level, they work as challenging puzzles. You are given a position and an accompanying task, such as “White to play and mate in two moves,” that must be fulfilled. On a higher level, problems are creative works designed to show an interesting – the composition’s main idea. How exactly are themes artistic? It varies, but important factors include subtlety, elegance, economy, paradox, and unity of play. The latter concept of unity is especially noteworthy; most good problems have multiple variations that are related to each other in some way, to create a harmonious impression.
Chess problems come in a variety of genres, the most common of which is the . In this type, White plays first and forces mate in the specified number of moves, against any black defence. Only one of White’s moves is able to achieve this, and the solver’s goal is to discover this unique first move, called the . If another move, unintended by the composer, solves the problem too, that alternative move is called a , and the problem becomes unsound. Such faulty problems, however, are rarely seen nowadays (especially in directmates) because of the practice of computer-testing, which ensures that cooks are eliminated.
1. Otto Wurzburg
American Chess Bulletin 1942, 3rd Hon. Mention
Mate in 2
Let’s examine our first sample of a . Problem 1's of “Mate in 2” indicates that it’s a directmate and White must mate by the second move. The solution begins with 1.Kc2! – the '!' signifies it's the key-move – after which the is 2.Sb3 mate. Black can parry this threat with various , but these moves allow White to mate in other ways. For instance, 1…bxc3 2.Bxc3; the two moves here, Black’s defence and White’s correct response, constitute a . The main variations of this problem are 1…Bf5+ 2.Se4, 1…R5g2+ 2.S3e2, and 1…R1g2+ 2.S1e2. These three lines represent the thematic play because they share a number of features: Black gives check but also unguards a white piece (rook or bishop) that’s training on the black king, enabling White to answer the check by interposing a knight, and to mate by discovery at the same time. Such a tactic, in which White stops a check by interposition, and gives check as well with the same move, is called a , and its recurring use is the theme of this problem.
Some conventions apply to key-moves in directmates, and knowing them will assist you when solving this type of problem. The desired feature of subtlety means that keys are very unlikely to be checks. Keys that capture a piece are almost unheard of, for the same reason, though the capture of a pawn is acceptable. In contrast to obviously aggressive first moves that are frown upon, keys that apparently weaken White or strengthen Black are viewed as good in the artistic sense. A perfect illustration is Problem 1, which has an excellent key because it exposes the white king to numerous checks. Though not all directmates are successful in incorporating them, you should keep in mind the possibility of such counter-intuitive first moves.
2. Murray Marble
La Stratégie 1908, 1st Prize
Mate in 2
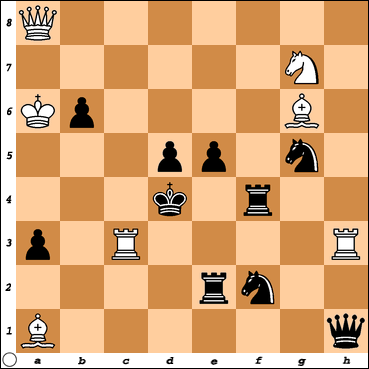
Problem 2 provides another example of a first-rate key: 1.Be4!, which sacrifices the bishop to seven black pieces. To deal with the threat of 2.Qxd5, Black must capture the key-piece, and the seven captures all lead to different mates. First, 1…Kxe4 self-pins the d5-pawn and enables a , 2.Rc4. The remaining defences involve , when Black obstructs the king’s on e4, preventing its escape to that square. 1…Qxe4 2.Rc2, 1…Rexe4 2.Rc1, 1…Rfxe4 2.Sf5, 1…Sgxe4 2.Se6, 1…Sfxe4 2.Rhd3, and 1…dxe4 2.Qd8.
Looking at the problems in this article, you may be struck by how the positions (unlike most tactical puzzles) seem far removed from actual games. That only highlights how problem composition is a field distinct from the competitive game. Chess problems are constructed in accordance with their own artistic principles. A particularly important one of such principles is economy of force, which holds that for any given idea shown in a problem, the amount of force used should be minimised, and that every piece must serve to bring about that idea or to ensure soundness. That the resulting problem positions do not resemble game situations is regarded as irrelevant. Nevertheless, another convention of problems links them directly to the game. Problem positions are required to be legal, i.e. they could have arisen from the opening array, however unlikely the players’ moves may have been in reaching these positions.
3. Richard Grewe, Fritz Karge & Hans Voigt
Die Schwalbe 1940
Mate in 2

When analysing a problem, it's always necessary to consider whether the key creates a threat or sets up a . The former is already illustrated in the first two diagrams, which are threat-problems. In block-problems, the key carries no threat but is a that puts Black in zugzwang. In such a position, every possible move by Black entails some weakness, which becomes exploitable by White because Black is compelled to move. Problem 3 is an example. Its key 1.Qe8! doesn’t threaten an immediate mate, but waits for Black to place the king in a weaker position. The king has four diagonal moves, and all result in different mates – this is the star-flights theme. 1…Kh6 2.Qg6, 1…Kh4 2.Qh5, 1…Kf6 2.Qe7, and 1…Kf4 2.Qe3. Note that the white queen initially controls h6, h4, and f6, so the generous key grants three flight-squares to the black king.
4. Jeremy Morse
(after J. C. J. Wainwright)
London Evening News 1960

Mate in 2

Problem 4 is also solved by a waiting key, 1.Rd1! Now most of Black’s moves simply unguard squares on which the white queen could give mate, and the point of the problem lies in the remarkable number of queen mates delivered. 1…Sxd1 2.Qf1, 1…Sd3 2.Qxd3, 1…a5 2.Qb5, 1…b5 2.Qc5, 1…c2 2.Qxc2, 1…Bf7 2.Qxf7, 1…Be6 2.Qxe6, 1…Bd5 2.Qxd5, 1…Rg4 2.Qxg4, 1…Rf4 2.Qxf4, 1…Re4 2.Qxe4, and 1…Be7/Bf6/Bg5 2.Qc8. These twelve variations with distinct queen mates represent a record for two-move problems. There are some non-thematic variations or : 1…Rd4/Rxh5 2.Rd4 and 1…Bc7 2.Rxh4.
5. Alain White
Good Companions 1918, 1st Prize
Version by R. Cabral

Mate in 2
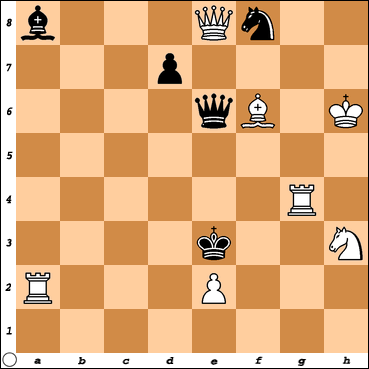
Problem 5 has rich play that involves pinning and unpinning effects. The white queen has its black counterpart pinned, and the latter in turn pins the white bishop, which could otherwise mate on d4 or g5. The key is 1.Qe7!, threatening 2.Qc5. Every move by the black queen defeats the threat, but also unpins the white bishop, hence 1…Qxe7 2.Bd4 and 1…Qe5 2.Bg5. After 1…Qe4, however, neither bishop mate works because the black queen has cut off the white rook’s control of d4. But this defence permits 2.Rg3, because the pinned queen has also interfered with the black bishop on the long diagonal. Two further thematic variations are 1…d6 2.Qa7 and 1…d5 2.Qa3. In each case the black pawn closes a defensive line of the black queen, which could therefore be unpinned with impunity by the white queen in the mating move.
6. Lev Ilich Loshinski
The Problemist 1930

Mate in 2

Problem 6 is for you to solve. The thematic play involves black self-interferences as well as the openings of white lines by black pieces.
Solution
Problem 6 solution (To display, hold down your mouse button and select the text below.)
>The key is 1.Qf2!, with the threat of 2.Qxa7. Black has five defences occurring on the same square, d4, where each defender interferes with a line controlled by the h4-rook or the a1-bishop. 1…d4 2.Bc4, 1…Rd4 2.Rh6, 1…Bd4 2.Qxe2, 1…Sed4 2.Qa2, and 1…Sfd4 2.Ra3. All of the black moves, except for 1…Bd4, also open a line that is traversed by the mating piece, an effect that adds to the unity of the variations.<
... |
附件: 你需要登錄才可以下載或查看附件。沒有帳號?註冊 |













 狗仔卡
狗仔卡








 分享
分享 收藏
收藏 支持
支持 提升卡
提升卡